++ 50 ++ 円錐 高さ 公式 308541

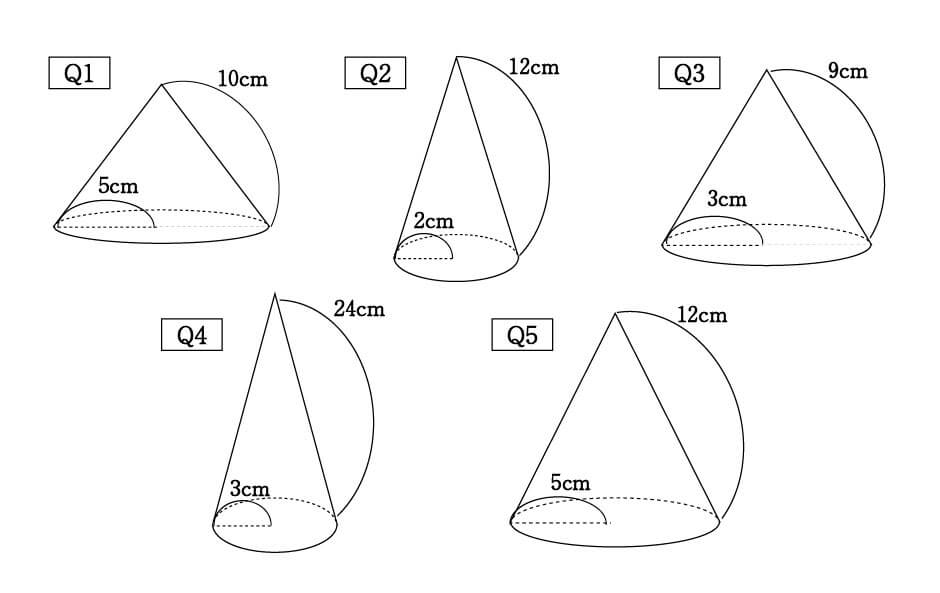
三平方の定理を利用して四角すい 円すいの体積を求める 無料で使える中学学習プリント
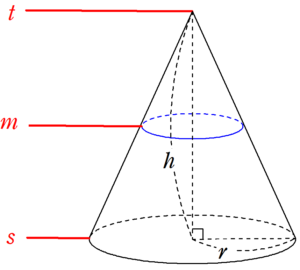
円錐の体積の公式 V = (1/3)π* r^2 * h (1) を出発点として考えることにします。 使うのは円錐の高さhではなくて母線の長さエルですが、エルが数字の1と紛らわしいのでここではエルのかわりにpを使うことにします。 p^2 = r^2 h^2 (2) です。 ここで条件は、p円錐の体積の求め方 公式と計算例 Scipursuit 体積の求め方 円錐 円錐の体積を求める公式は、次の通りです。 V = 1 3Sh = 1 3πr2h V = 1 3 S h = 1 3 π r 2 h ここで、V は円錐の体積、S は底面積、h は高さを表します。 また、2行目における π は円周率、r は底面の
円錐 高さ 公式
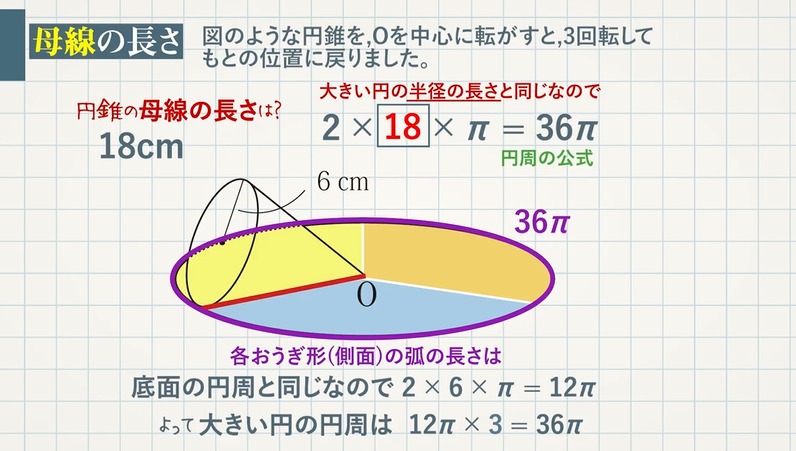
円錐 高さ 公式- 円柱の体積=底面積×高さなので 答え 197cm³ スポンサードリンク 問題③ 体積が628cm³である次の円柱の高さを求めましょう。 (円周率は314とします。) 《円柱の高さの求め方》 円柱の体積=底面積×高さであることから問題図のような円錐を、Oを中心に転がすと、 $\textcolor{green}{3}$ 回転してもとの位置に戻りました。 円錐の母線の長さを求めなさい。 $3$ 回転ということは、中心がOである 大きい円の円周 は、 側面のおうぎ形 $\textcolor{blue}{3}$ 枚分の長さ と等しくなります。
積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典
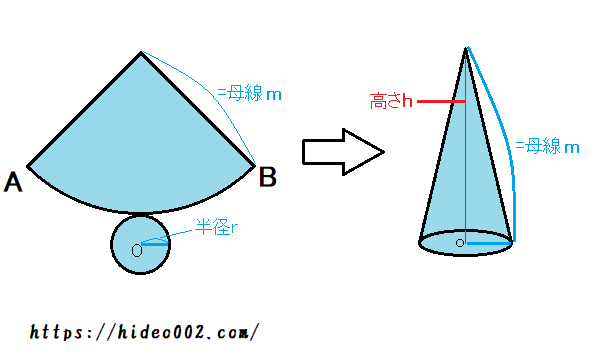
直円錐の体積 簡単で短時間に間違いなく計算ができ非常に便利このサイトよく使用していますよ。 大きな土の山が有り、どけて欲しいという要請が有り、土の量を計算したかった。 底が楕円として、楕円錐の体積を算出したかった。 長径a,短径bの楕円 円錐の体積の求め方公式 円錐の体積は、次の公式で求められます。 円錐の体積=底面積×高さ÷3 円錐の底面積は円の面積ですので、円の面積×高さ÷3で求めることができます。 ⇒ 円の面積の求め方 スポンサードリンク円錐の場合も同様に、展開図を書いて考えてみましょう。 ここでは、公式化するために、底面の半径 r 、母線の長さ R の円錐を考えます。 底面の半径 r、母線の長さ R の円錐 円錐の展開図を理解する上で大事なポイントは次の3点です。
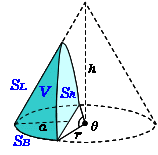
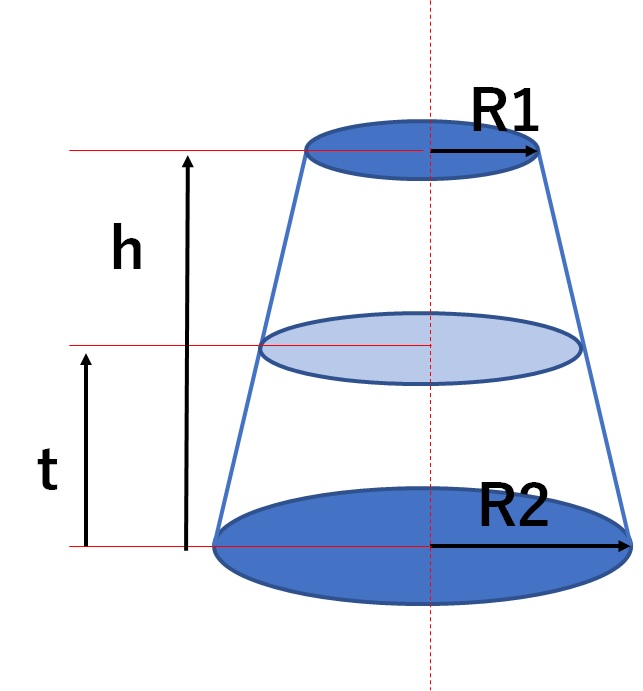
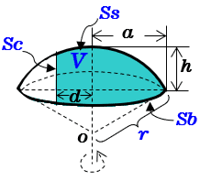
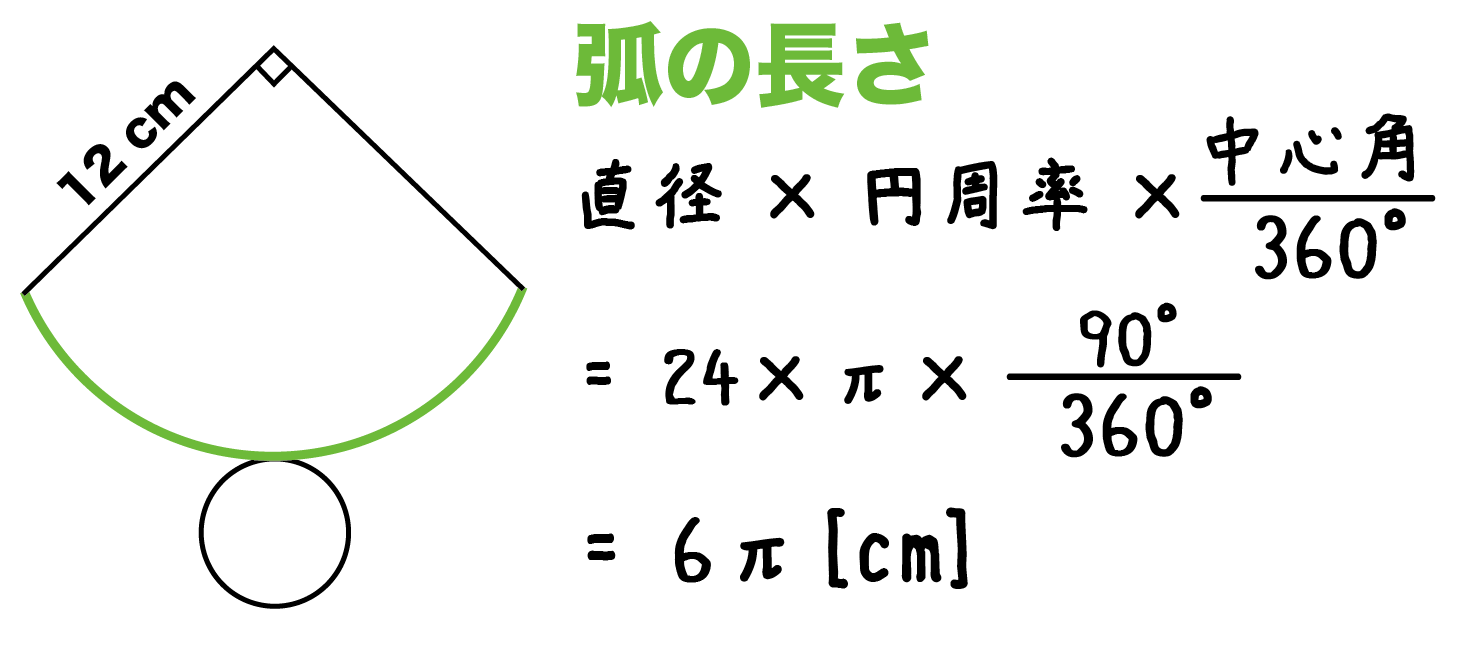
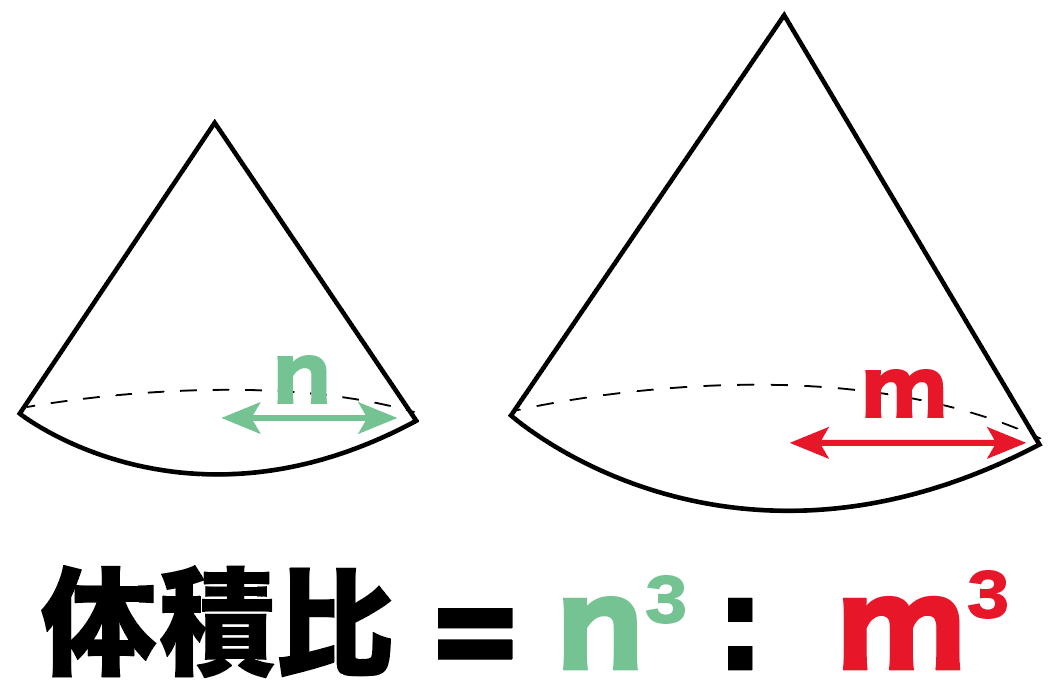
公式を覚えなくても、おうぎ形の弧の長さと底円の円周の長さが等しい事を使って計算できます。 また、$2\times314$の 計算を後回し にし、 分数の分母分子で消して やると、 結局は公式と同じ計算 になります。まずは、容器全体の大きさを求めるために 大きな円錐と、水が入っている部分の小さい円錐に注目します。 それぞれの立体の高さが より 相似比は となります。 よって、体積比は3乗の値を考えて となります。 水が入っている円錐は体積が3㎝³なの円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S
円錐 高さ 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
「円錐 高さ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「円錐 高さ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「円錐 高さ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「円錐 高さ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「円錐 高さ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「円錐 高さ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円錐 高さ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「円錐 高さ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「円錐 高さ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「円錐 高さ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「円錐 高さ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
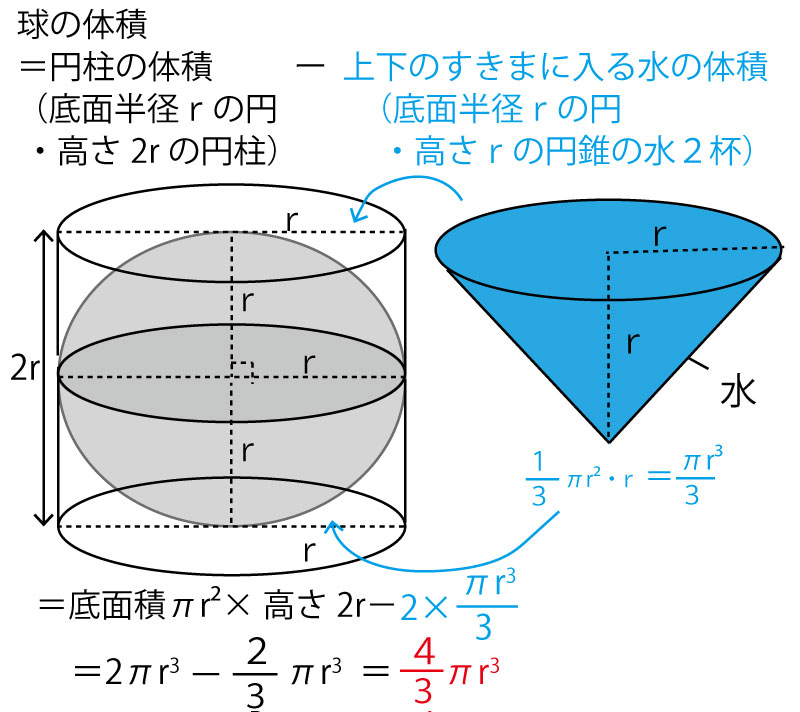
あれ、さっきの半球の体積は、底面が円で高さrの円錐の2倍ですよ。 円錐×2=半球 円錐×3=円柱 ということですか。 T:つまり、cがaに対して何倍になっているのかで、1/2か、1/3か、2/3かが決まるということです。 円錐の中心角の求め方概要 扇部分の半径 (母線)・弧の長さを求める (扇の中心角を求める問題になる) 中心角を求める こんな感じだよ 既に知ってる「扇の中心角を求める問題」に変えてしまう っていうのがポイント! 扇の中心角の求め方を知らない人
コメント
コメントを投稿